Los triángulos son de las figuras más conocidas en el mundo de la geometría: se sabe que poseen tres lados y ciertas características específicas que los singularizan. A continuación, como en ningún otro sitio, presentamos clasificación e imágenes de triángulos para compartir.
Clasificación de triángulos según sus lados
Posiblemente el triángulo sea de los polígonos más sencillos, pero siempre su correcta comprensión ayuda con otros de mayor complejidad. En definitiva, la geometría se cimenta en ese paso paso necesario de lo más simple a lo complejo.
Existen diversas clasificación del triángulo y una de ellas se fundamenta en los lados. De acuerdo a los lados los triángulos pueden ser: equilátero, isósceles y escaleno.
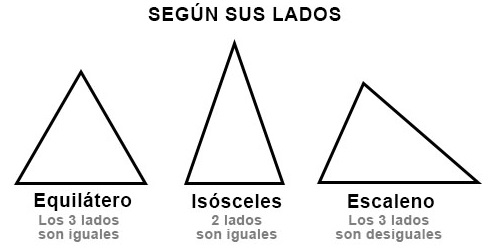
- Triángulo equilátero: En geometría el triángulo equilátero es un polígono regular y como su nombre lo indica sus tres lados son iguales.
- Triángulo isósceles: El triángulo isósceles es aquel que tiene dos lados iguales (igualdad de longitud) y otro no. El ángulo formado por los dos lados iguales de longitud se denomina vértice y el lado opuesto es la base.
- Triángulo escaleno: El triángulo escaleno es un polígono con la característica de poseer los tres lados diferentes.
Clasificación de triángulos según sus ángulos
Pero los lados no refieren a la única forma de caracterizar a los triángulos, ya que también se pueden clasificar de acuerdo a los ángulos.
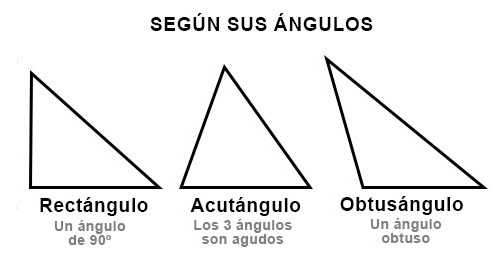
- Triángulo rectángulo: Dos de sus lados forman un ángulo recto, es decir, (lo que es lo mismo) forman un ángulo de 90 grados.
- Triángulo acutángulo: Todos sus ángulos son agudos o, lo que es lo mismo, todos sus ángulos miden menos de 90 grados.
- Triángulo escaleno obtusángulo: Dos de sus lados forman un ángulo obtuso o tienen un ángulo de más de 90 grados, lo que es lo mismo.
Elementos de un triángulo
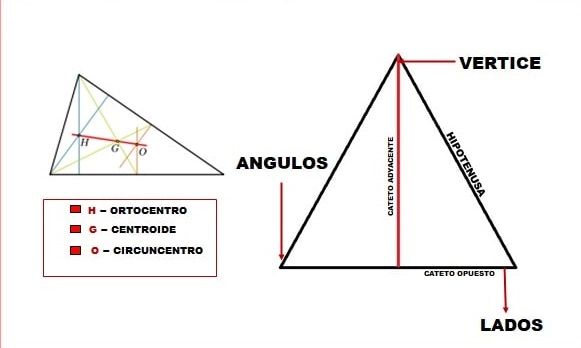
Un triángulo está conformado por diferentes elementos. Desde la sencillez (los primeros que vienen a la mente) podemos decir que en esencia los triángulos tienen lados, vértices y ángulos. Esos rasgos hacen que todo triángulo lo sea efectivamente: hacen a la esencia del triángulo en tanto objeto ideal-geométrico.
- Lados: Son un total de tres y lo constituyen las rectas que forman al polígono.
- Vértices: Son un total de tres y hacen alusión a los puntos donde se unifican dos lados.
- Ángulos: Tiene un total de tres el triángulo y son una suerte de aberturas que se forman al unirse dos lados (se miden en grados, tomando como totalidad los 360).
Área de un triángulo
Naturalmente, se puede calcular el área del triángulo. El área o superficie de un triángulo cualquiera es el producto de la base por la altura dividido por dos.
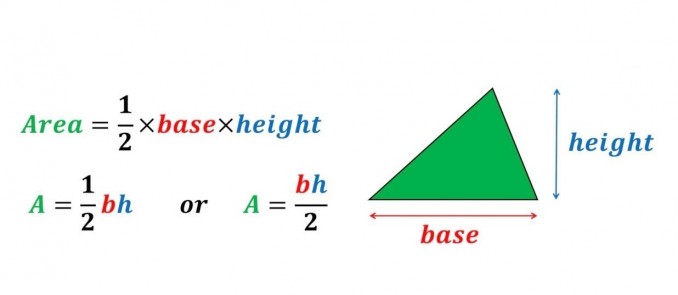
Por supuesto, dependiendo del triángulo el área se calculará de una manera diferente.
Triángulo equilátero
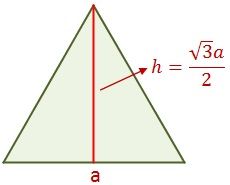
El triángulo escaleno tiene los tres lados iguales. Su área, como en todo triángulo, será el medio de la base por su altura. El triángulo equilátero se lo define por la siguiente fórmula.
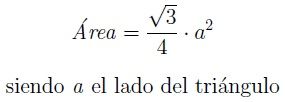
Triángulo isósceles
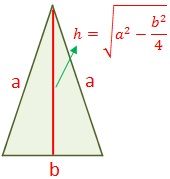
El área de un triángulo isósceles será un medio de la base por su altura. En triángulo isósceles puede calcularse por medio de la siguiente fórmula.
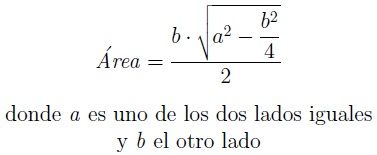
Triángulo escaleno
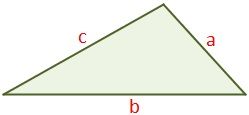
El área del triángulo escaleno puede calcularse mediante la fórmula de Herón (en alusión a Herón de Alejandría) si se conocen todos sus lados (a, b y c). Entonces la fórmula sería la siguiente.

Ahora también existe otra manera de obtener el área de un triángulo escaleno. La figura necesaria se emplaza abajo para clarificar.
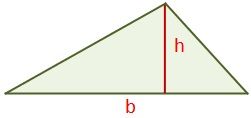
Es decir, también se puede calcular si se conoce un lado b y la altura h, que está asociada a dicho lado. La formula sería la siguiente.
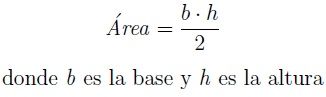
Teoremas de los triángulos
Los triángulos en la geometría son de estudio recurrente. Por supuesto que poseen sus propias fórmulas y teoremas. Hay que entender a estos últimos como una proposición (una propuesta matemática) que puede demostrarse. Entonces, un teorema certero no importa las veces que se lo ponga a prueba: siempre llegará al mismo resultado.
En los teoremas de triángulos se evalúan proposiciones que mediante ciertos cálculos se comprueba su veracidad. Estos son una multitud y a continuación disponemos algunos de ellos.
- Teorema de los ángulos interiores: En todo triángulo cuando se suman las medidas de los ángulos interiores siempre se consigue un total de 180 grados. Esto se confirma con la suma de cada uno de los lados.
- Teorema de la medida de un ángulo exterior: Aquí hay algo de mayor complejidad, pero básicamente cuando se suman los ángulos exteriores de los triángulos el resultado de las medidas es la suma de dos ángulos interiores.
- Teorema de los ángulos exteriores: Este teorema nos recalca que la suma de las medidas de los ángulos exteriores, teniendo en consideración el vértice (vital para calcular un ángulo exterior) suma un total de 360 grados.
- Teorema de las longitudes: La longitud que se encuentra en un lado tiene que ser mayor a la diferencia entre longitudes de los otros dos lados. Mientras que, a su vez, será menor que la suma de las mismas.
- Teorema de la altura: Este teorema nos dice que en cada triángulo rectángulo la altura será relativa a la hipotenusa. De acuerdo a la media proporcional de los segmentos que dividen a la hipotenusa.
- Teorema del cateto: En un triángulo rectángulo el cateto será la media proporcional a la hipotenusa.
- Teorema de Pitágoras: En todos los triángulos rectángulos el cuadrado de la hipotenusa (lado opuesto al ángulo recto de un triángulo rectángulo) será igual a la suma de los cuadrados de las longitudes de los catetos (los lados menores del triángulo rectángulo). La fórmula es la siguiente: c2=a2 + b2.